Samlamb Chaturbhuj ka kehsetrafal, Parimap Formula:- समलम्ब चतुर्भुज को english में Trapezium कहते हैं. अतः समलम्ब चतुर्भुज एक ऐसा चतुर्भुज होता है जिसमे की (चार भुजावों) में कोई दो विपरीत भुजा समान्तर होती हैं तथा दो अन्य भुजाये समान्तर नहीं होती हैं. समलम्ब चतुर्भुज पर आधारित बेसिक सवाल या प्रश्न कक्षा 9 तथा कक्षा 10 के परीक्षा में पूछे जाते हैं. अतः यह जरुरी है कि Samlamb Chaturbhuj की सभी मूल जानकारियों को जाने. जैसे कि समलम्ब चतुर्भुज का चित्र कैसा होता है, इसका क्षेत्रफल का सूत्र, परिमाप का फार्मूला, परिभाषा तथा गुण क्या होता है.
आज के इस लेख में Trapezium से सम्बंधित जानकारियों को साझा किया हूँ, जिससे की RRB, NTPC, SSC तथा अन्य सहयोगी परिक्षावों की तैयारी कर रहे स्टूडेंट्स के लिए लाभकारी हो. अतः लेख को अंत तक पढ़ें.
Table of Contents
Samlamb Chaturbhuj का मूल जानकारी – परिभाषा एवं फार्मूला
समलम्ब चतुर्भुज क्या है या किसे कहते हैं (परिभाषा):- “समलम्ब चतुर्भुज एक ऐसा चार भुजावों वाली ज्यामिति आकृति होता है जिसमे की दो सम्मुख भुजावों का युग्म समान्तर होता है एवं दो अन्य भुजाएं असमांतर व असमान होती हैं.” जैसा कि नीचे समलम्ब चतुर्भुज का चित्र दिया हुआ है.
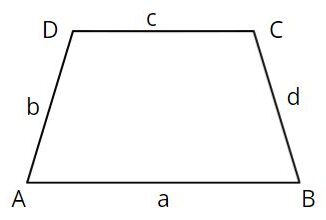
समलम्ब चतुर्भुज के असमांतर भुजावों को सामान तथा समांतर करने पर अन्य चतुर्भुज का रूप ले लेती हैं. अतः अगर किसी चतुर्भुज के भुजावों, कोणों तथा माप में परिवर्तन किया जाये तो निम्न प्रकार के samlamb chaturbhuj का निर्माण होगा. जैसे की समकोण समलम्ब चतुर्भुज, समद्विबाहु समलम्ब चतुर्भुज, विषम बाहू समलम्ब चतुर्भुज.
| सम चतुर्भुज का क्षेत्रफल | वर्ग का क्षेत्रफल का फार्मूला |
| चक्रीय चतुर्भुज की परिभाषा | समबाहु त्रिभुज का क्षेत्रफल |
| गोले का आयतन | शंकु के सूत्र |
समलम्ब चतुर्भुज – क्षेत्रफल, परिमाप, ऊँचाई का सूत्र
किसी भी समलम्ब चतुर्भुज के क्षेत्रफल का सूत्र, परिमाप, विकर्ण का फार्मूला तथा ऊँचाई आदि निकालने के लिए समलम्ब चतुर्भुज के चित्र को समझना होगा. अतः माना कि एक Samlamb Chaturbhuj है जिसकी भुजावों का माप a, b, c तथा d है जैसा की नीचे दिए चित्र में देख सकते हैं.
1. क्षेत्रफल का सूत्र / फार्मूला

समलम्ब चतुर्भुज के क्षेत्रफल निकालने के लिए उस चतुर्भुज के समान्तर सम्मुख भुजावों का माप तथा चतुर्भुज की ऊँचाई पता होना चाहिए. अतः
समलम्ब के क्षेत्रफल का फोर्मुला = (1/2) x (समान्तर भुजावों का योग) x ऊँचाई
दिए गए चित्र से भुजा तथा ऊँचाई का माप लेने पर,
Area of Trapezium (A) = (1/2) x (a + c) x h
2.परिमाप का सूत्र – Samlamb Chaturbhuj
किसी भी द्विविमीय ज्यामिति आकृति के भुजावों का योग निकालने पर उस आकृति का परिमाप निकाल सकते हैं. अतः समलम्ब का परिमाप निकालने के लिए चतुर्भुज के समान्तर भुजावों तथा असमांतर भुजावों का योग ज्ञात करना होगा. अतः,
समलम्ब के परिमाप का फार्मूला = सभी भुजावों का योग
Perimeter of Trapezium = (AB + BC + CD + CA) = (a + b + c + d)
3.ऊँचाई | Height
एक समलम्ब चतुर्भुज की ऊँचाई कैसे निकालते हैं उसकी दो विधियों को नीचे बताया गया है जो की इस प्रकार से है.

a) जब समलम्ब चतुर्भुज का क्षेत्रफल दिया हो.
माना कि समलम्ब चतुर्भुज का क्षेत्रफल A है तथा दोनों समान्तर भुजावों की माप a तथा b है. तब
समलम्ब चतुर्भुज की ऊँचाई (h) = (2 x क्षेत्रफल) / (समान्तर भुजावों का योग) = 2A / (a + c)
b) जब समलंब चतुर्भुज की भुजाएं दी हो
माना की samlamb chaturbhuj की भुजाएं a, b, c तथा d है तथा अर्द्ध परिमाप s है. जैसा कि नीचे दिए हुए चित्र में देख सकते हैं. तब,
- अर्द्ध परिमाप s = 1/2(a + b + d – c) जब भुजा (a) भुजा (c) से बड़ी हो अर्थात (a > c)
समलम्ब की ऊँचाई का सूत्र,

- अर्द्ध परिमाप s = 1/2(c + b + d – a) जब भुजा (c) भुजा (a) से बड़ी हो अर्थात (c > a)
समलम्ब चतुर्भुज की ऊँचाई,
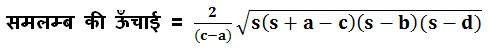
समलम्ब चतुर्भुज की विशेषताएं | Properties
एक समलम्ब चतुर्भुज का गुणधर्म:- किसी भी समचतुर्भुज की निम्नलिखित विशेताएँ होती हैं जिन्हें की याद रखना काफी जरुरी है.
- समलम्ब चतुर्भुज के किन्ही दो सम्मुख भुजायें एक दुसरे के समान्तर होती हैं, जबकि अन्य दो भुजाएं असमांतर होती हैं.
- यदि समलम्ब चतुर्भुज के दोनों असमांतर भुजावों का माप बराबर हो जाये तथा दोनों भुजाये आधार भुजा से सामान कोण बनाये तो वह एक समद्विबाहु समलम्ब चतुर्भुज कहलाता है.
- यदि समलम्ब चतुर्भुज की दोनों असमांतर भुजाये एक दुसरे के समान्तर हो जाये तो वह एक समान्तर चतुर्भुज होगा.
- समलम्ब चतुर्भुज के विकर्ण सदैव एक दुसरे को समद्विभाजित करते हैं.
- यदि समलम्ब के चारों शीर्ष कोण समकोण हो जाते हैं तो वह एक आयत होगा अथवा एक वर्ग होगा.
- समलम्ब चतुर्भुज के विकर्ण के मध्य बिंदु को मिलाने वाली रेखा की लम्बाई = 1/2 x (दोनों समान्तर भुजावों का घटाव)
- समलम्ब चतुर्भुज के असमांतर भुजावों के मध्य-बिंदु को मिलाने वाली रेखाखंड की लम्बाई = 1/2 x (दोनों समान्तर भुजावों का योग)
Samlamb Chaturbhuj के कुछ मुख्य सिद्धांत
माना कि एक समलम्ब चतुर्भुज है जिसकी भुजाएं AB, BC, CD तथा DA है. जैसा की चित्र में देख सकते हैं कि चतुर्भुज के विकर्ण एक दुसरे को O पर समद्विभाजित कर रहे हैं. अतः
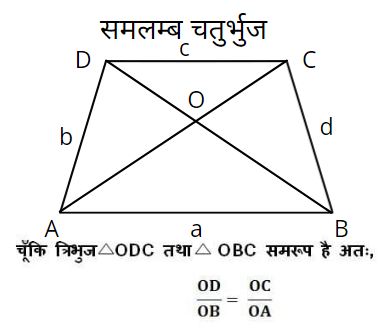
चूँकि एक ही आधार पर बने विभिन्न त्रिभुजों का क्षेत्रफल सामान होता है अतः, त्रिभुज ACB का क्षेत्रफल त्रिभुज ABD के क्षेत्रफल के बराबर होगा.
△ACB का क्षेत्रफल = △ABD का क्षेत्रफल
साथ ही त्रिभुज △AOD का क्षेत्रफल त्रिभुज △BOC के क्षेत्रफल के बराबर होगा. ध्यान रहे इस पर अक्सर परिक्षावों में बहुविकल्पीय प्रश्न पूछे जाते हैं.
समलम्ब चतुर्भुज के भुजावों का मध्य बिंदु
1.) यदि samlamb chaturbhuj के दोनों असमांतर भुजावों के मध्य बिंदु को मिला दे, तो रेखाखंड की लम्बाई निम्नलिखित सूत्र से निकाल सकते हैं.
असमांतर भुजावों के मध्य बिंदु को मिलाने वाली रेखाखंड की लम्बाई = 1/2 x ( दोनों समान्तर भुजावों का योगफल)
2.) किसी समलम्ब चतुर्भुज के विकर्ण (Diagonals) के मध्य बिंदु को मिलाने वाली रेखा खंड की लम्बाई नीचे दिए फार्मूला से निकाल सकते हैं.
समलम्ब चतुर्भुज के दोनों विकर्ण के मध्य बिंदु को मिलाने वाली रेखाखंड की लम्बाई = 1/2 x (समान्तर भुजावों का घटाव)
सारांश – समलम्ब चतुर्भुज की ऊँचाई, क्षेत्रफल, परिमाप
मुझे आशा है कि ऊपर दिए गए सभी जानकारियों को आप समझ गए हैं. विद्यार्थी गण समलम्ब चतुर्भुज के निम्नलिखित जानकारियों द्वारा अपने परीक्षा में पूछे गए सम्बंधित सवालों को हल कर सकते हैं. अगर किसी विद्यार्थी को इस लेख से सम्बंधित कुछ पूछना हो तो कमेंट बॉक्स में पूछ सकता है या अपना सुझाव भी दे सकते हैं.
“इस वेबसाइट (careerkhojo.com) पर शिक्षा से सम्बंधित जानकारियों को साझा किया जाता है. अतः इस वेबसाइट की जानकारियों को अपने दोस्तन के साथ शेयर कर सकते हैं.”
