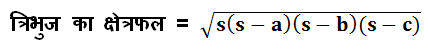[फ़ॉर्मूला] त्रिभुज का क्षेत्रफल : सूत्र, परिभाषा, परिमाप | Area of Triangle in Hindi

त्रिभुज का क्षेत्रफल Tribhuj ka kshetrafal (Area of Triangle in Hindi)

Tribhuj ka kshetrafal ka sutra formula | त्रिभुज का क्षेत्रफल का परिभाषा (Tribhuj ka kshetrafal Ka Definition) | त्रिभुज का क्षेत्रफल का सूत्र, Area of Triangle in Hindi | Tribhuj Formula | समद्विबाहु त्रिभुज का क्षेत्रफल का सूत्र, त्रिभुज का क्षेत्रफल का सूत्र | विषमबाहु त्रिभुज का क्षेत्रफल | समबाहु त्रिभुज का क्षेत्रफल क्या होता है|त्रिभुज का क्षेत्रफल और परिमाप, त्रिभुज का क्षेत्रफल formula |त्रिभुज का क्षेत्रफल फार्मूला एवं महत्वपूर्ण गुण (Tribhuj ka kshetrafal)  त्रिभुज का क्षेत्रफल (Tribhuj ka kshetrafal) :- त्रिभुज का क्षेत्रफल व परिमाप का फ़ॉर्मूला/सूत्र क्या होता है? (AREA OF TRIANGLE) त्रिभुज का क्षेत्रफल की परिभाषा क्या होती है? त्रिभुज कितने प्रकार के होते है? अक्सर ऐसे त्रिभुज से सम्बंधित प्रश्न हमारे परीक्षावों पूछे जाते हैं. आज के इस लेख में त्रिभुज से संबधित कुछ गुणों को परिभाषित करेंगे. जैसे कि त्रिभुज का क्षेत्रफल का सूत्र (AREA OF TRIANGLE FORMULA), त्रिभुज का परिमाप का सूत्र, Tribhuj ka kshetrafal कितने तरीकों से निकाल सकते है इत्यादि.

Tribhuj ka kshetrafal त्रिभुज का क्षेत्रफल : परिभाषा, प्रकार, परिमाप 

त्रिभुज का क्षेत्रफल का फार्मूला ज्ञात होने से पहले हमे त्रिभुज से जुड़े कुछ जरुरी तथ्यों को जान लेना जरुरी है. त्रिभुज के इन सभी जरुरी चीजों को जान लेने के बाद त्रिभुज का एरिया और परिमाप निकालना आसान हो जायेगा.  त्रिभुज किसे कहते हैं?  “तीन भुजावों अथवा रेखाखंडों से घिरी हुयी द्विआयामी समतल आकृति त्रिभुज कहलाती है. एक त्रिभुज में तीन भुजाएं, तीन कोण तथा तीन शीर्ष होते हैं.” 

त्रिभुज का क्षेत्रफल की परिभाषा: सूत्र, प्रकार (Formula of Area of Triangle, Definition & Types of Triangle)

Tribhuj ka kshetrafal :- त्रिभुज एक द्विविमीय आकृति होती है जो कि तीन रेखाखंड से घिरी होती है. त्रिकोण त्रिभुज का क्षेत्रफल ज्ञात करने करने के लिए त्रिभुज के भुजावों, कोणों का मान, त्रिभुज का प्रकार, त्रिभुज की आधार से लम्बवत ऊँचाई, त्रिभुज के शीर्षों का निर्देशांक ज्यामिति आदि का पता होना जरुरी है.  साधारणतः त्रिभुज का क्षेत्रफल ज्ञात करने के लिए ये फार्मूला ज्यादातर प्रयोग में लाया जाता है.  त्रिभुज का क्षेत्रफल = (½) × आधार × ऊँचाई = (½) × B × H 1. त्रिभुज की लम्बवत ऊँचाई (H) = (2 × त्रिभुज का क्षेत्रफल)/ आधार  2. त्रिभुज का आधार (B) = (2 × त्रिभुज का क्षेत्रफल)/ ऊँचाई   किन्तु त्रिभुज का आकार बदलने पर बेसिक त्रिभुज के क्षेत्रफल सूत्र को प्रयोग नहीं कर सकते है. अतः सर्वप्रथम त्रिभुज के प्रकार कितने होते है वो जान लेते है, फिर उसके आधार पर त्रिभुज का क्षेत्रफल ( Tribhuj ka kshetrafal Formula) ज्ञात करेंगे.

A.) भुजावों के आधार पर त्रिभुज का प्रकार और उसका क्षेत्रफल 

भुजावों अथवा रेखाखंडों के आधार पर त्रिभुज को 3 भागों में विभाजित किया जाता है जो कि इसप्रकार है.

1.) समबाहु त्रिभुज (Area of Equilateral Triangle) : परिभाषा, परिमाप और समबाहु त्रिभुज का क्षेत्रफल

एक समबाहु त्रिभुज की तीनो भुजाएं परस्पर बराबर होती है. साथ ही समबाहु त्रिभुज के तीनो शीर्ष कोण भी बराबर होते है और प्रत्येक कोण 60०  का होता है. माना कि समबाहु त्रिभुज है जिसकी प्रत्येक भुजा का परिमाण “a” है तथा तीनो कोण 60० के है. जैसा कि नीचे दिए गए चित्र में देख सकते है. चित्र में देख सकते है कि एक शीर्ष लम्ब कोण A से आधार BC पर बिंदु D पर मिल रहा है. जैसा कि हम जानते है त्रिभुज का क्षेत्रफल = (½) × आधार × ऊँचाई = (½) × BC × AD  ………(1) अतः  पाइथागोरस प्रमेय के अनुसार त्रिभुज Δ ABD में, AB² = BD² + AD² AD²  = AB² – BD² AD²  = a² – (a/2)² AD = √(3a²/4) = √3 a/2 समीकरण (1) से, 

• समबाहु त्रिभुज का क्षेत्रफल (sambahu tribhuj ka kshetrafal) = (½) × BC × AD  समबाहु त्रिभुज का क्षेत्रफल = √3 a² /4
• समबाहु त्रिभुज का परिमाप = a + a + a = 3 × भुजा (a)

2.) समद्विबाहु त्रिभुज (Area of Isosceles Triangle Formula) : परिभाषा, परिमाप और समद्विबाहु त्रिभुज का क्षेत्रफल

एक समद्विबाहु त्रिभुज की दो भुजाएं तथा दो कोण आपस में बराबर होती है. माना कि एक समद्विबाहु त्रिभुज है जिसकी दो बराबर भुजा “a” है तथा तीसरी भुजा “b” है. एक लम्बवत रेखा शीर्ष कोण A से आधार BC पर बिंदु D पर मिलता है जो कि BC रेखा को दो बराबर भागों (b/2) में विभाजित करता है. अतः  पाइथागोरस प्रमेय के अनुसार त्रिभुज Δ ABD में, AB² = BD² + AD² AD²  = AB² – BD² AD²  = a² – (b/2)² AD = √{a² – (b²/4)}

• समद्विबाहु त्रिभुज का क्षेत्रफल (samdibahu tribhuj ka kshetrafal) = (½) × BC × AD 
• समद्विबाहु त्रिभुज का क्षेत्रफल का सूत्र  = ½ × b × √{a² – (b²/4)}
• समद्विबाहु त्रिभुज का परिमाप का सूत्र = (2a + b)

3.) विषमबाहू  त्रिभुज (Area of Scalene Triangle Formula) : परिभाषा, परिमाप और विषमबाहू त्रिभुज का क्षेत्रफल

विषम बाहू त्रिभुज की तीनो भुजाएं असमान होती है, साथ ही तीनो शीर्ष कोण भी असमान होते है. विषमबाहू त्रिभुज का क्षेत्रफल हेरॉन फ़ॉर्मूला (Heron’s Formula) से निकला जाता है. माना कि एक त्रिभुज है जिसकी भुजाएं a, b व c हैं.  हीरोन का सूत्र (Area of scalene triangle by Heron’s Formula)  जहाँ, त्रिभुज का अर्द्ध परिमाप S = (a + b + c)/2

B.) कोणों के आधार पर त्रिभुज का प्रकार और उसका क्षेत्रफल 

कोणों के आधार पर त्रिभुज को तीनो भागों में विभाजित किया जाता है. 

• समकोण त्रिभुज परिभाषा एवं क्षेत्रफल का सूत्र 
• न्यून कोण त्रिभुज परिभाषा एवं क्षेत्रफल का सूत्र 
• अधिक कोण त्रिभुज परिभाषा एवं क्षेत्रफल का सूत्र 

1.) समकोण त्रिभुज (Area of Right Angle Triangle Formula) : परिभाषा, परिमाप और समकोण त्रिभुज का क्षेत्रफल

समकोण त्रिभुज में एक कोण 90०  का होता है बाकि के दो कोण न्यून कोण होते है. समकोण त्रिभुज में 90०  के सामने वाली भुजा कर्ण होती है, बाकि की दो भुजाएं आधार व लम्ब होती है. समकोण त्रिभुज का सबसे ज्यादा उपयोग त्रिकोणमिति में होता है. यदि समकोण त्रिभुज में दो भुजाएं आपसे में बराबर होती है तो वो समकोण समद्विबाहु त्रिभुज कहलाता है. साथी ही बाकि के दो कोणों का मान 45० होता है.

• समकोण त्रिभुज का क्षेत्रफल (samkon tribhuj ka kshetrafal) = (½) × आधार × ऊँचाई = √3/4 × भुजा²
• समकोण समद्विबाहु त्रिभुज का क्षेत्रफल (samkon samadwibahu tribhuj ka kshetrafal) = (½) × भुजा²
• परिमाप =भुजावों का योग 
• समकोण समद्विबाहु त्रिभुज का परिमाप = (√2 + 2) × भुजा 

मेंसुरेशन फार्मूला इन हिंदी PDF

2.) न्यून कोण तथा अधिक कोण त्रिभुज का क्षेत्रफल : परिभाषा, परिमाप 

न्यून कोण त्रिभुज :-  न्यून कोण कोण त्रिभुज में प्रत्येक तीनो कोण शुन्य से अधिक तथा 90० से कम होता है. साथ ही तीनो कोणों का योग 180० होता है. न्यून कोण त्रिभुज का क्षेत्रफल भी हीरोन के क्षेत्रफल सूत्र से ही निकालते है. अधिक कोण त्रिभुज :- अधिक कोण त्रिभुज में एक कोण 90० से होता है. साथ ही अधिक कोण त्रिभुज में तीनो कोणों का योग 180० होता है.  न्यून कोण व अधिक कोण त्रिभुज का क्षेत्रफल हीरोन के क्षेत्रफल सूत्र से निकालते है.  1. अधिक कोण व न्यून कोण त्रिभुज का क्षेत्रफल (हीरोन का सूत्र )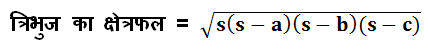 

2. त्रिभुज का परिमाप = भुजावों का योग (a+b+c) 3. त्रिभुज का क्षेत्रफल = (½) × आधार × ऊँचाई (जब त्रिभुज की लम्बवत ऊँचाई दी हो) 4. त्रिभुज का अर्द्ध परिमाप S = (a + b + c)/2  नोट :- यदि किसी त्रिभुज के तीनो शीर्ष का निर्देशांक ज्यामिति दिया हो, तब त्रिभुज का क्षेत्रफल (tribhuj ka kshetrafal) निकालने का तरीका – माना कि किसी त्रिभुज के तीनो शीर्षों का निर्देशांक  (X_{1 ,} Y₁), (X_2 , Y₂), (X_3 , Y₃)  Δ त्रिभुज का क्षेत्रफल = ½ [X₁ (Y₂ – Y₃) + X₂ (Y₃ – Y₁) + X₃ (Y₂ -Y₁)]

त्रिभुज का क्षेत्रफल के सूत्र पर आधारित कुछ प्रश्न 

1.) एक त्रिभुज के भुजावों का मान क्रमशः 6 सेमी, 8 सेमी व 10 सेमी  है. त्रिभुज का क्षेत्रफल क्या होगा? माना कि भुजाएं a = 6 सेमी, b = 8 सेमी, c = 10 सेमी  अतः हिरोन फार्मूला,

त्रिभुज का अर्द्ध परिमाप S = (a + b + c)/2 = (24/2) = 12  त्रिभुज का क्षेत्रफल = √(12-6)(12-8)(12-10) = 4√3 सेमी² 2.) एक समकोण समद्विबाहु त्रिभुज का क्षेत्रफल व कर्ण का माप ज्ञात करिए जिसकी भुजा का परिमाण 6 सेमी है? माना कि भुजा a = 6 सेमी  समकोण समद्विबाहु त्रिभुज का क्षेत्रफल (samkon samadwibahu tribhuj ka kshetrafal) = (½) × भुजा² त्रिभुज का क्षेत्रफल = ½ × (6×6) = 18 वर्ग सेमी  कर्ण की लम्बाई = √2 × भुजा = 6√2 सेमी  3.) एक समबाहु त्रिभुज का परिमाप 120 सेमी है। समकोंण त्रिभुज का क्षेत्रफल क्या होगा? समबाहु त्रिभुज का परिमाप = 3 × भुजा = 120  भुजा = 120/3 = 40 सेमी  समकोण त्रिभुज का क्षेत्रफल = √3/4 × भुजा^{2 =} = √3/4 ×40 ×40 = 400√3 वर्ग सेमी  Tags:-त्रिभुज का क्षेत्रफल का सूत्र उदाहरण Tribhuj ka kshetrafal ka formula (chetrafal),त्रिभुज का क्षेत्रफल का सूत्र (Tribhuj ka kshetrafal ka formula), समकोण त्रिभुज का क्षेत्रफल (Samkon Tribhuj ka Chetrafal), sambahu tribhuj ka kshetrafal, samdibahu tribhuj ka kshetrafal