मेंसुरेशन फार्मूला इन हिंदी पीडीएफ डाउनलोड 2023 Mensuration formula in Hindi

मेंसुरेशन/क्षेत्रमिति फार्मूला हिंदी (All mensuration formula in Hindi & English)

All mensuration formulas class 8| क्षेत्रमिति के सभी सूत्र डाउनलोड | mensuration formula for class 10| mensuration formulas class 9 |mensuration formulas for class 6| मेंसुरेशन फार्मूला इन हिंदी पीडीऍफ़ डाउनलोड | all mensuration formulas in maths | all mensuration formula pdf | list of all mensuration formulas | mensuration formula in Hindi pdf download| क्षेत्रमिति के सभी सूत्र pdf|क्षेत्रमिति सूत्र pdf download | क्षेत्रमिति का सूत्र | mensuration all formula in Hindi pdf download| mensuration formulas tricks and tips | Mensuration Formula pdf download for all board and other exams| क्षेत्रमिति सूत्रों की सूची पीडीऍफ़ |mensuration 2d and 3d formula pdf in hindi |क्षेत्रफल का सूत्र pdf download 2D और 3D के लिए

All mensuration formula pdf Hindi English

मेंसुरेशन फार्मूला इन हिंदी pdf download:- दोस्तों, गणित में मेंसुरेशन सूत्र (Mensuration formula in Hindi) की मदद से द्विविमीय तथा त्रिविमीय आकृतियों का क्षेत्रफल तथा आयतन बहुत आसानी से निकाल सकते है. चूँकि द्विविमीय तथा त्रिविमीय आकृतियों से सम्बंधित प्रश्न हमारे प्रतियोगी परिक्षावों में पूछे जाते है, अतः मेंसुरेशन/क्षेत्रमिति का फार्मूला याद रखना बहुत महत्वपूर्ण है.

क्षेत्रमिति के सवाल कई बोर्ड स्कूलों में कक्षा 6 से ही बेसिक लेवल पर ही शुरू कर दी जाती है. अतः इस पोस्ट में बेसिक लेवल से उच्च लेवल तक की Mensuration formula को संलग्न किया गया है. इस पोस्ट में Mensuration Formula for Class 8 तथा  Mensuration Farmula for Class Class 10 के अलावा प्रतियोगी परिक्षावों में पूछे जाने वाले प्रश्नों पर आधारित मेंसुरेशन फार्मूला को भी सम्मलित किया  है.

Mensuration formula pdf in Hindi & English
मेंसुरेशन फार्मूला इन हिंदी PDF Download

विद्यार्थी गण अपने सुविधा के लिए मेंसुरेशन फार्मूला हिंदी और इंग्लिश का PDF Download भी यहाँ से कर सकते है. इस मेंसुरेशन फार्मूला PDF फाइल में हिंदी व इंग्लिश दोनों भाषावों का प्रयोग किया गया है.

मेंसुरेशन/क्षेत्रमिति सूत्र दो आयामी आकृतियों के लिए (Mensuration formula for two dimensional shapes in Hindi)

Area and volume formulas in hindi for 2-D structure

A. त्रिभुज आकृति (Triangle Shape)

तीन भुजावों से घिरी हुई बंद आकृति को त्रिभुज कहते हैं. एक त्रिभुज में तीन भुजाएं, तीन कोण तथा तीन शीर्ष होते है. त्रिभुज के तीनो आंतरिक कोणों का योग 180° डिग्री होता है.

1. समबाहु त्रिभुज (Equilateral triangle)

एक समबाहु त्रिभुज की तीनो भुजाएं सामान होती है अर्थात तीनों भुजावों का परिमाण बराबर होती है. साथ ही समबाहु त्रिभुज के प्रत्येक  कोण का मान 60° अंश होता है.

समबाहु त्रिभुज का परिमाप (Perimeter of Equilateral tringle)= (भुजा + भुजा + भुजा) = 3 × भुजा 

समबाहु त्रिभुज का क्षेत्रफल(Area of Equilateral Triangle):- 

2. समद्विबाहु त्रिभुज (Isoceles tringle):- 

एक समद्विबाहु (Isoceles) त्रिभुज में कोई दो भुजाये तथा सम्मुख कोण आपस में बराबर होते है. अगर एक समद्विबाहु त्रिभुज की भुजाएं a, a, b है तब, 

समद्विबाहु त्रिभुज का परिमाप (Perimeter of Isoceles tringle) = (2a + b)

समद्विबाहु त्रिभुज का क्षेत्रफल(Area of Isoceles Triangle):- 

3. समकोण त्रिभुज (Right Angle Triangle) :-

एक समकोण त्रिभुज में एक कोण 90° अंश का होता है बाकि के दो कोण न्यून कोण होते हैं.

समकोण त्रिभुज का परिमाप (Perimeter of Right Angle tringle) = (a + b + c)

समकोण त्रिभुज का क्षेत्रफल(Area of Right Angle Triangle):- 

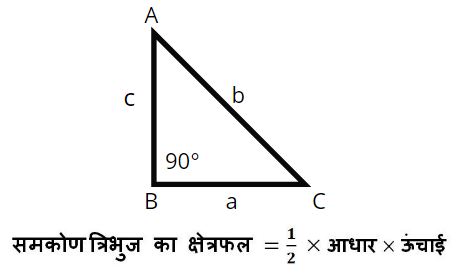
नोट:- समद्विबाहु समकोण त्रिभुज का क्षेत्रफल = ½ × a²

4. विषमबाहु त्रिभुज (Asymmetrical Triangle) :-

ऐसा त्रिभुज जिसकी तीनो भुजाएं तथा तीनो कोण विषम हो अथवा अलग-अलग हो, विषमबाहु त्रिभुज कहलाता है.

विषमबाहु त्रिभुज का परिमाप (Perimeter of Asymmetrical tringle) = (a + b + c)

विषमबाहु त्रिभुज का क्षेत्रफल(Area of Asymmetrical Triangle)

B. चतुर्भुज आकृति (Quadrilateral Shape)

चतुर्भुज किसे कहते हैं:- चतुर्भुज चार भुजावों से घिरा हुआ एक बंद आकृति है. एक चतुर्भुज में चार भुजायें तथा चार शीर्ष होते है. साथ ही चतुर्भुज के अन्तः कोणों का योग 360° होता है. 

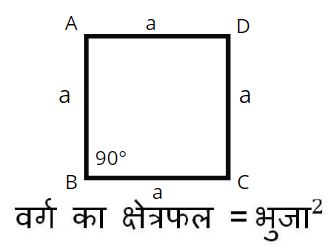
1. वर्ग (Square):- 

(Square) वर्ग एक समांतर चतुर्भुज है जिसमें की चारों भुजायें सामान होती है अर्थात चारों भुजावों की लम्बाई बराबर होती है. साथ ही वर्ग में प्रत्येक शीर्ष कोण 90° होता है.

वर्ग का परिमाप (Perimeter of Square) = 4 × भुजा 

वर्ग का क्षेत्रफल (Area of Square):-

2. आयत (Rectangle):- 

(Rectangle) आयत एक समांतर चतुर्भुज है जिसमे की आमने सामने की भुजाये बराबर (समांतर) होती है. साथ ही आयत की प्रत्येक शीर्ष कोण 90° होता है.

आयत का परिमाप (Perimeter of Rectangle) = 2 × (लम्बाई +चौडाई) 

आयत का क्षेत्रफल (Area of Rectangle):-

3. समांतर चतुर्भुज (Parallelogram):- 

समांतर चतुर्भुज की आमने सामने की भुजायें बराबर व समानांतर होती है.

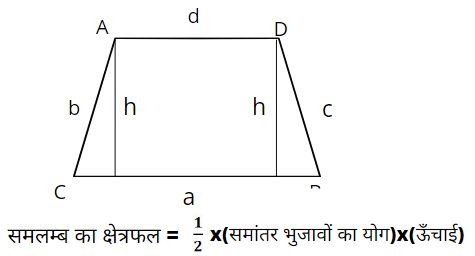
3. समलम्ब चतुर्भुज (Trapezium):- 

(Trapezium) समलम्ब चतुर्भुज चार भुजावों वाली एक द्विविमीय आकृति है जिसमे की कोई दो आमने सामने (सम्मुख) भुजावों का युग्म समांतर व असमान होती है.

समलम्ब चतुर्भुज का परिमाप (Perimeter of Trapezium) = भुजावों का योग (a+b+c+d) 

समलम्ब चतुर्भुज का क्षेत्रफल (Area of Trapezium):-

4. समचतुर्भुज (Rhombus):- 

यह एक समान्तर चतुर्भुज होता है जिसमे की चारों भुजाएं आपस में बराबर होती है तथा विकर्ण एक दुसरे को 90° कोण पर समद्विभाजित करते है.

समचतुर्भुज का परिमाप (Perimeter of Rhombus) = भुजावों का योग (4 x भुजा) 

समचतुर्भुज चतुर्भुज का क्षेत्रफल (Area of Rhombus):-

दिए गए चित्र में विकर्ण D तथा d है.

C. वृत आकृति (Circular Shape)

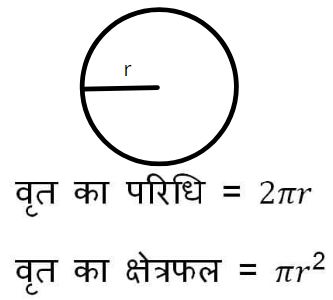
1. वृत (Circle):- 

किसी भी निश्चित बिंदु से सामान दूरी पर स्थित बिन्दुवों का बिन्दुपथ या (locus) वृत कहलाता है. निश्चित बिंदु वृत का केंद्र कहलाता है.

वृत का परिधि (Circumference of Circle) = 2πr 

वृत का क्षेत्रफल (Area of Circle):-

2. अर्द्धवृत (Semi-Circle):- 

अर्द्धवृत का कुल परिधि (Circumference of Circle) = (πr + 2r)

मेंसुरेशन/क्षेत्रमिति सूत्र त्रि-आयामी आकृतियों के लिए (Mensuration formula for three dimensional shapes in Hindi)

Area and volume formulas in hindi for 3-D structure

1. घन (Cube):-

घन एक त्रिविमीय ज्यामिति आकृति है जिसमे की लम्बाई, चौड़ाई व ऊँचाई बराबर होती है. साथ ही एक घन में 12 किनारे, छः फलक व आठ कोर्नर (कोने) होते है.

घन का क्षेत्रफल व आयतन (Area and Volume of cube):- 

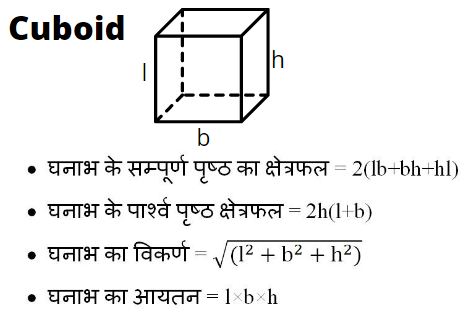
2. घनाभ (Cuboid):-

घनाभ एक त्रिविमीय ज्यामिति आकृति है जिसमे छः फलक होते है जो की आयताकार होते है.

घनाभ का क्षेत्रफल व आयतन(Area and Volume of cuboid):- माना की घनाभ की लम्बाई l, चौड़ाई b तथा ऊँचाई h है.

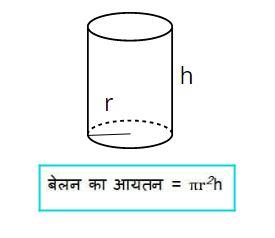
3. बेलन  (Cylinder):- 

अगर किसी आयत की एक भुजा को स्थिर रखकर दुसरे विपरीत भुजा को चारों तरफ (360°) तक घुमाने पर जो काल्पनिक आकृति  बनती है उसे बेलन कहते है. 

माना की एक बेलन है जिसकी त्रिज्या “r” है तथा ऊँचाई “h”.

बेलन का क्षेत्रफल व आयतन (Area and Volume of cylinder)

घुमावदार (वक्रपृष्ठ ) सतह का क्षेत्रफल = 2πrh

सम्पूर्ण पृष्ठ का क्षेत्रफल = 2πr(r+h)

खोखला बेलन  (Hollow Cylinder):- 

माना कि एक खोखला बेलन है जिसकी बाह्य त्रिज्या “R” तथा आतंरिक त्रिज्या “r” है. बेलन की ऊँचाई “h” है.

खोखला बेलन का क्षेत्रफल व आयतन(Area and Volume of Hollow cylinder)

• घुमावदार (वक्रपृष्ठ ) सतह का क्षेत्रफल = बाह्य पृष्ठ + आतंरिक पृष्ठ = 2πRh + 2πrh
• सम्पूर्ण पृष्ठ का क्षेत्रफल = 2π(R+r)(h+R-r)
• खोखले बेलन का आयतन = बाह्य आयतन – आंतरिक आयतन 
• 

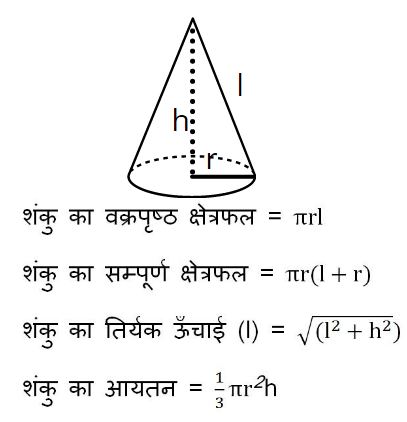
4. शंकु  (Cone):- 

एक समकोण त्रिभुज को अपनी ऊर्ध्वाधर रेखा के परितः घुमाकर बनाई गई आकृति एक शंकु है।

शंकु का क्षेत्रफल व आयतन(Area and Volume of Cone)

मानाकि की शंकु की आधार त्रिज्या = r
ऊँचाई (height) =h
तिर्यक ऊँचाई (slant height) = l

शंकु का क्षेत्रफल व आयतन :- 

4. ठोस गोला (Solid Sphere):- 

गोला एक त्रिविमीय ठोस आकृति होती है. जब किसी वृताकार परत को उसके व्यास के परितः 360° तक घुमाये तो गोला बनता है.

मानाकि एक ठोस गोला है जिसकी त्रिज्या एवं व्यास R व D है.

गोले का क्षेत्रफल व आयतन (Area and Volume of Sphere) :- 

मेंसुरेशन फार्मूला इन हिंदी PDF Download All mensuration formulas pdf in Hindi & English Click Here Download PDF

चाल और वेग में मुख्य अन्तर

निष्कर्ष :- (मेंसुरेशन फार्मूला इन हिंदी PDF Download)

मुझे आशा है की ऊपर दिए गए All mensuration formula in Hindi & English pdf| Mensuration All Formula PDF Download  आपके सेमेस्टर, वार्षिक तथा प्रतियोगी परीक्षायों के लिए काफी लाभदायक  होगी. अगर इस ऊपर मेंसुरेशन अथवा क्षेत्रमिति के फार्मूला में किसी प्रकार की दिक्कत है तो कमेंट बॉक्स में पूछ  सकते है.

Tags:-
मेंसुरेशन फार्मूला इन हिंदी PDF, मेंसुरेशन फार्मूला इन हिंदी PDF Download, क्षेत्रमिति के सभी सूत्र, क्षेत्रमिति के सभी सूत्र PDF Download, क्षेत्रफल का सूत्र pdf, क्षेत्रफल का सूत्र PDF Download , Mensuration formula PDF, Mensuration all formula