कक्षा 10 निर्देशांक ज्यामिति का परिचय, सूत्र | Nirdeshank Jyamiti Formula in Hindi

निर्देशांक ज्यामिति फार्मूला l निर्देशांक ज्यामिति सूत्र pdf l निर्देशांक ज्यामिति / कक्षा 10 l निर्देशांक क्या है। Nirdeshank Jyamiti Formula in Hindi

Coordinate Geometry Formula in Hindi:- निर्देशांक ज्यामिति को एक कक्षा 9 तथा10 के विद्यार्थियों के अति महत्वपूर्ण अध्याय है. Nirdeshank Jyamiti से काफी अच्छे प्रश्न बनते हैं जो कि सरल होते हैं जिससे की परिक्षावों में ज्यादा अंक अर्जित किया जा सकता है. निर्देशांक ज्यामिति (Coordinate Geometry) पर आधारित प्रश्नों को हल करने से पहले विद्यार्थियों को इसकी मूल जानकारियों को जानना अति आवश्यक है.

अतः इस पोस्ट में इस अध्याय से सम्बंधित जानकारियों को साझा किया गया है, जैसे कि निर्देशांक ज्यामिति क्या है तथा इसके सूत्र क्या है. या निर्देशांक ज्यामिति के सूत्रों के आधार पर त्रिभुज का क्षेत्रफल कैसे निकाले, दिए हुए दो बिन्दुवों के बीच दूरी का फार्मूला क्या है या रेखाखंड विभाजन सूत्र क्या है इत्यादी?

Coordinate geometry in Hindi | Nirdeshank Jyamiti, परिभाषा एवं फ़ॉर्मूला

निर्देशांक ज्यामिति परिभाषा, विशेषता एवं फार्मूला:- निर्देशांक ज्यामिति अध्याय के सवालों को हल करने से पहले यह जरुरी है कि इस प्रसंग के सभी मूल जानकारियों को जान ले. अतः यहाँ पर सभी जानकारियों को चित्र तथा परिभाषा के माध्यम से समझाया गया है अतः ध्यानपूर्वक पढ़ें.

निर्देशांक ज्यामिति परिभाषा | Definition of Coordinate Geometry in Hindi

“जब हम ज्यामिति का अध्ययन बिन्दुवों की स्थिति या विशिष्ट संख्यावों द्वारा (जिन्हें निर्देशांक कहते हैं) निरुपित कर के विभिन्न ज्यामिति आकृति या वक्रों के आधार पर करते हैं, निर्देशांक ज्यामिति या वैश्लेषिक ज्यामिति कहलाती है.“

निर्देशांक ज्यामिति से जुड़े मुख्य परिभाषाएं

किसी भी ज्यामिति आकृति को अगर निर्देशांक ज्यामिति के आधार पर समझना है तो कुछ महत्वपूर्ण परिभाषावों को जानना अति आवश्यक है.

1. कार्तीय निर्देश तंत्र (Cartesian Coordinate System):- किसी भी ज्यामिति आकृति को बिन्दुवों के आधार पर समझने के लिए तथा उन बिन्दुयों की स्थिति को व्यक्त या निरुपित करने के लिए एक प्रणाली या व्यवस्था को तैयार किया गया जिसे कार्तीय निर्देश तंत्र (प्रणाली) कहते हैं. इसको निचे दिए गए चित्र तथा परिभाषा के माध्यम से भी समझ सकते हैं.

” किसी समतल में दो परस्पर लम्बवत रेखाखंड या रेखावों के प्रतिच्छेदन से बना प्रणाली या तंत्र कार्तीय निर्देश तंत्र (प्रणाली) कहलाता है.” इसे अन्य नामों से भी जाना जाता है जैसे कि समतलीय या आयतीय निर्देश तंत्र. जैसा कि नीचे दिए गए चित्र में देख सकते हैं कि रेखा XOX^‘ तथा YOY^‘ एक दुसरे को परस्पर लम्बवत प्रतिच्छेद कर रहे हैं.

2. निर्देशांक अक्ष (Coordinate axis):- कार्तीय निर्देश तंत्र की क्षैतिज तथा उर्ध्वाधर रेखावों (जो की XOX^‘ तथा YOY^‘ लम्बवत हैं) को निर्देशांक अक्ष कहते हैं. दिए गए चित्र में देख सकते हैं, क्षैतिज रेखा (XOX^‘) को x-अक्ष तथा उर्ध्वाधर रेखा (YOY^‘) को य-अक्ष कहते हैं.

3. निर्देशांक (Co-ordinate):- समतल में या निर्देशांक अक्ष पर स्थित प्रत्येक बिंदु के स्थिति को किसी ना किसी विशिष्ट संख्या द्वारा प्रदर्शित किया जाता है जिसे उस बिंदु का निर्देशांक (Coordinate) कहते हैं.

4. चतुर्थांश (Quadrant):- जैसे कि नाम से ही प्रतीत हो रहा चतुर्थ अंश (अथवा चौथा भाग). अतः निर्देशांक ज्यामिति अक्ष एक समतल को चार भागों में विभाजित करते हैं. इन चारों चतुर्थांश को प्रथम चतुर्थांश, द्वितीय चतुर्थांश, तृतीय चतुर्थांश तथा चतुर्थ चतुर्थांश नाम दिया गया है.

चतुर्थांश	संकेत	क्रमित युग्म
प्रथम चतुर्थांश	( +, + )	( +x , +y )
द्वितीय चतुर्थांश	( – , + )	( -x , +y )
तृतीय चतुर्थांश	( – , – )	( -x , -y )
चतुर्थ चतुर्थांश	( + , – )	( +x , -y )

5. भुज (Ordinate) :- क्षैतिज रेखा (XOX^‘) अथवा x-अक्ष पर स्थित सभी बिंदु को एक किसी ना किसी संख्या द्वारा निरुपित या प्रदर्शित किया जाता है. अर्थात x-अक्ष पर स्थित सभी बिन्दुवों को x-निर्देशांक या भुज कहते हैं.

6. कोटि (Abscissa):- उर्ध्वाधर रेखा (XOX^‘) अथवा y-अक्ष पर स्थित बिन्दुवों को एक विशिष्ट संख्या द्वारा निरुपित या प्रदर्शित किया जाता है, जिसे कोटि या y-निर्देशांक कहते हैं.

7. क्रमित युग्म :- चतुर्थांश के किसी भी भाग में या XY समतल पर स्थित किसी भी बिंदु के स्थिति को प्रदर्शित करने के लिए x-निर्देशांक तथा y-निर्देशांक को हमेशा एक युग्म में लिखते हैं, जिसे क्रमित युग्म कहते हैं. अर्थात किसी भी ज्यामिति आकृति या वक्र पर स्थित बिंदु को व्यक्त करने के लिए भुज तथा कोटि के क्रमित युग्म का उपयोग करेंगे.

8. मूल बिंदु (Origin Point):- जिस बिंदु पर क्षैतिज x-अक्ष तथा उर्ध्वाधर y-अक्ष एक दुसरे को प्रतिच्छेद करते हैं उसे मूल बिंदु कहते हैं. इस बिंदु को क्रमित युग्म (0 , 0) से व्यक्त करते हैं.

दो बिन्दुवों के बीच के दूरी का सूत्र | Distance Formula

माना कि एक कार्तीय समतल है जिसमे की दो बिन्दुवों के निर्देशांक {x₁ , y₁} तथा {x₂ , y₂} दिए हुए हैं. तब उन बिन्दुवों के बीच दूरी निम्नलिखित सूत्र के द्वारा निकाल सकते हैं.

दूरी का सूत्र = √(x₂ – x₁)² + (y₂ – y₁)² = √(x₁ – x₂)² + (y₁ – y₂)²

प्रश्न:- दिए गए बिन्दुवों के बीच की दूरी ज्ञात करिए. P (2 , 4) तथा Q (7 , 8)

माना कि x₁ = 2, y₁ = 4, x₂ = 7, y₂ = 8

दोनों बिन्दुवों के बीच की दूरी = √(x₂ – x₁)² + (y₂ – y₁)² = √(7 – 2)² + (8 – 4)² = 5 यूनिट

अन्तः तथा बाह्य विभाजन सूत्र | Section Formula

किसी दो विन्दुवों को मिलाने वाली रेखा को यदि कोई बिंदु m:n अनुपात में अन्तः विभाजित या बाह्य विभाजित करता है तो उस बिंदु का निर्देशांक निम्नलिखित सूत्रों द्वारा ज्ञात किया जा सकता है.

1.अन्तः विभाजन फार्मूला या सूत्र

माना कि दो बिन्दुवों को मिलाने वाली रेखा AB है जिसको कि एक बिंदु m:n के अनुपात में अन्तः विभाजित करता है. इस स्थिति में उस बिंदु का निर्देशांक निम्नलिखित सूत्र की मदद से ज्ञात कर सकते हैं.

माना दी हुयी रेखा के बिंदु A {x₁ , y₁} तथा B {x₂ , y₂} है. साथ ही जो बिंदु अन्तः विभाजित करता है उसका निर्देशांक (X , Y) है. तब

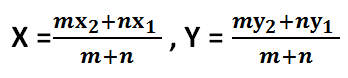
नोट:- यदि दो बिन्दुवों को मिलाने वाली रेखा के मध्य-बिंदु को निकालना हो तो इस सूत्र से निकाल सकते हैं.

दो बिन्दुवों को मिलाने वाली रेखा के मध्य बिंदु का सूत्र

X = (x₁+x₂) / 2 , Y = (y₁+y₂) / 2

2. बाह्य विभाजन फार्मूला

निचे दिए गए चित्र में देख सकते हैं कि एक रेखा AB जिसके निर्देशांक A {x₁ , y₁} तथा B {x₂ , y₂} है. वह बिंदु जो रेखाखंड को बाह्यतः m:n के अनुपात में विभाजित करता है तो उस बिंदु निर्देशांक निम्न सूत्र के द्वारा निकाल सकते हैं. माना कि बाह्य बिंदु C का निर्देशांक (X , Y) है.

निर्देशांक बिन्दुवों वाले त्रिभुज का क्षेत्रफल का सूत्र

निर्देशांक ज्यामिति त्रिभुज का क्षेत्रफल:- माना कि एक त्रिभुज है जिसके तीनो कोनो के निर्देशांक A (x₁ , y₁), B (x₂ , y₂), तथा C (x₃ , y₃) है. तब त्रिभुज का क्षेत्रफल का सूत्र –

नोट :- यदि दिए गए तीनो बिंदु संरेख (एक ही रेखा) में है उस स्थिति में त्रिभुज का निर्माण नहीं होगा. अतः त्रिभुज का क्षेत्रफल शुन्य होगा. इस प्रकार ऊपर दिए गए सूत्र में त्रिभुज के क्षेत्रफल का शुन्य रख कर अन्य सम्बन्ध निकाल सकते हैं.

Nirdeshank Jyamiti से जुड़े मुख्य बातें

• यदि एक रेखाखंड जिनके निर्देशांक A {x₁ , y₁} तथा B {x₂ , y₂} है और कोई एक बिंदु (x , y) रेखाखंड को m:n के अनुपात में विभाजित करता है तो तब m:n का अनुपात निम्नलिखित सूत्र से निकाल सकते हैं.

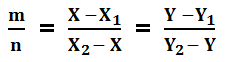
• यदि किसी भी बिंदु A का निर्देशांक (x , y) है तो उसे बिंदु को A (x , y) के तरह लिखते हैं.
• किसी बिंदु का x-निर्देशांक या भुज y-अक्ष से सदैव लम्बवत दूरी पर स्थित होता है.
• किसी बिंदु का y-निर्देशांक या भुज x-अक्ष से हमेशा लम्बवत दूरी पर स्थित होता है.
• यदि किसी भी निर्देशांक का भुज शुन्य (x = 0) हो जाये तो वह बिंदु y-अक्ष पर स्थित होगा.
• यदि किसी भी XY समतल में निर्देशांक का कोटि शुन्य (y = 0) हो जाये तो वह बिंदु x-अक्ष पर स्थित होगा.
• एक कार्तीय समतल में y-अक्ष का समीकरण x = 0 होता है. साथ ही x-अक्ष का समीकरण y=0 होता है.

अंत में – Nirdeshank Jyamiti | Co-ordinate Geometry

मुझे आशा है कि ऊपर दिए गए निर्देशांक ज्यामिति से जुड़े सभी मूल बाते आपको समझ में आ गयी होगी. जैसे कि मध्य बिंदु के निर्देशांक का सूत्र, निर्देशांक ज्यामिति के सूत्र, निर्देशांक ज्यामिति त्रिभुज का क्षेत्रफल, निर्देशांक ज्यामिति कक्षा 10th से जुडी परिभाषाएं, अन्तः और बाह्य विभाजन सूत्र का फार्मूला इत्यादी. अगर किसी भी विद्यार्थी को इससे सम्बन्धित किसी प्रकार का प्रश्न पूछना हो तो कम्मेंट बॉक्स में पूछ सकता है.

यह भी देखें:-

समलम्ब चतुर्भुज क्या है	चक्रीय चतुर्भुज के क्षेत्रफल का सूत्र
समचतुर्भुज के सूत्र	शंकु का क्षेत्रफल, आयतन
वर्ग का क्षेत्रफल और परिमाप	समबाहु त्रिभुज का क्षेत्रफल का सूत्र