Samantar chaturbhuj kshetrafal, Vikarn, paribhasha:- Samantar Chaturbhuj को इंग्लिश में Parallelogram कहते हैं. समान्तर चतुर्भुज एक ऐसा ज्यामिति आकृति जो की चार भुजावों से घिरा हुआ होता है जिसमे की सम्मुख भुजाएं समान्तर और बराबर होती हैं. इस चतुर्भुज पर आधारित प्रश्नों या सवालों को हल करने के लिए यह आवश्यक के विद्यार्थी गण समान्तर चतुर्भुज की मूल परिभाषा, चित्र, कोण, विकर्ण आदि को समझे. कक्षा 9 तथा कक्षा 10 के विद्यार्थियों को इस पर आधारित सिद्ध करने वाले सवाल भी पूछे जाते हैं.
अतः इस पोस्ट के जरिये यही बताने वाले हैं कि समांतर चतुर्भुज किसे कहते हैं, क्षेत्रफल का फार्मूला, विकर्ण का सूत्र, आसन्न कोण में सम्बन्ध क्या है. अतः इस पोस्ट को अंत तक अवश्य तक पढ़ें.
यह भी पढ़ें:-
| 1. चक्रीय चतुर्भुज का क्षेत्रफल | 2. समचतुर्भुज का क्षेत्रफल |
| 3. समलम्ब चतुर्भुज | 4. आयत का क्षेत्रफल सूत्र |
| 5. वर्ग का क्षेत्रफल | 6. निर्देशांक ज्यामित के फार्मूला |
Table of Contents
समान्तर चतुर्भुज का परिभाषा क्षेत्रफल, परिमाप, विकर्ण सूत्र
समांतर चतुर्भुज किसे कहते हैं या समान्तर चतुर्भुज को कैसे परिभाषित करे इसके लिए इस चतुर्भुज के चित्र को समझना काफी जरुरी है। Samantar Chaturbhuj के चित्र को समझने के बाद उससे जुड़ी मूल जानकारियां जैसे कि समांतर चतुर्भुज का क्षेत्रफल का सूत्र, परिमाप का सूत्र, विकर्ण का सूत्र, समांतर चतुर्भुज के गुण आदि समझ में आ जायेंगे।
Samantar Chaturbhuj का चित्र
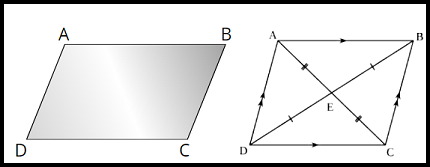
समांतर चतुर्भुज की परिभाषा । Definition of Parallelogram in Hindi
समांतर चतुर्भुज किसे कहते हैं, ” समांतर चतुर्भुज एक ऐसी द्वि-विमीय ज्यामिति आकृति है जिसमे के आमने सामने की भुजाएं सामान (बराबर) व समांतर होती है।” जैसा कि ऊपर दिए गए चित्र में देख सकते हैं कि आमने सामने की भुजाएं सामान व एक दुसरे के समांतर है।
साथ ही चित्र में देख सकते,
AB = DC एवं BC = AD
AB ll DC एवं BC ll DA
Samantar Chaturbhuj का क्षेत्रफल फार्मूला
Area of Parallelogram in Hindi:- एक समांतर चतुर्भुज का क्षेत्रफल निकालने के लिए उस चतुर्भुज के आधार का माप तथा लम्बवत ऊँचाई का मान पता होना जरुरी है। इसके अलावा यदि Samantar Chaturbhuj के चारों भुजवों का माप दिया हुआ है साथ ही उस चतुर्भुज के एक कोण का मान दिया हुआ है तो भी समांतर चतुर्भुज का क्षेत्रफल अन्य फार्मूला से निकाल सकते हैं। दोनों प्रक्रिया क्रमशः दिया हुआ है।
1.जब आधार एवं लम्बवत ऊँचाई का मान दिया हो
यदि एक समांतर चतुर्भुज के आधार भुजा की माप तथा लम्बवत ऊँचाई का माप दिया हो तो समांतर चतुर्भुज का क्षेत्रफल निम्नलिखित सूत्रों द्वारा निकाल सकते हैं।
माना कि समांतर चतुर्भुज के आधार का माप (a) तथा लम्बवत ऊँचाई (h) है, जैसा कि नीचे दिए गए चित्र में देख सकते है।

एक समांतर चतुर्भुज का क्षेत्रफल उस चतुर्भुज के आधार भुजा तथा लम्बवत ऊँचाई के गुणनफल के बराबर होता है। अर्थात,
समान्तर चतुर्भुज का क्षेत्रफल = आधार x लम्बवत ऊँचाई = a x h
2. जब दो आसन्न भुजावों के बीच का कोण तथा भुजावों का माप दिया हो
यदि किसी समांतर चतुर्भुज के दो समीपवर्ती भुजवों के बीच का कोण दिया हो तथा प्रत्येक भुजा की माप दी हो तो समान्तर चतुर्भुज का सूत्र निम्नलिखित तरीके से निकाल सकते हैं।
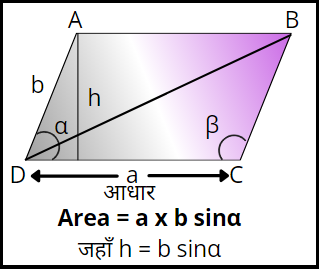
जैसा कि ऊपर दिए गए चित्र में देख सकते हैं कि दो आसन्न भुजावों के बीच का कोण (α) है, तब समांतर चतुर्भुज का क्षेत्रफल निम्नलिखित सूत्र से निकाल सकते हैं।
समान्तर चतुर्भुज का क्षेत्रफल = आधार x लम्बवत ऊँचाई = a x b sinα
समान्तर चतुर्भुज का परिमाप या परिमिति।Samantar Chaturbhuj ka Parimap formula
Perimeter of Parallelogram in Hindi:- किसी भी द्वि-विमीय ज्यामिति आकृति (बहुभुज) के सभी भुजावों का योग निकालें तो वह उसका परिमाप होगा। यदि समान्तर चतुर्भुज के परिमाप को ज्ञात करना है तो सभी भुजावों के परिमाण का योग करना होगा।
माना कि एक Samantar Chaturbhuj है जिसकी आधार भुजा (a) तथा आसन्न भुजा (b) है तब,
समांतर चतुर्भुज का परिमाप = चारों भुजावों का योग = 2 (a + b)
समांतर चतुर्भुज से जुड़ी मूल जानकारियां
किसी भी समांतर चतुर्भुज के प्रश्न को हल करने से पहले यह जानना जरुरी है कि समांतर चतुर्भुज के कोणों तथा भुजवों में क्या सम्बन्ध होता है। सभी डिटेल नीचे दिए गए हैं।
- AB = DC एवं BC = AD
- AB ll DC एवं BC ll DA
- ∠A + ∠B + ∠C + ∠D = 360०
- ∠ A = ∠C एवं ∠B = ∠D
- ∠A + ∠B = ∠C + ∠D = ∠B + ∠C = ∠D + ∠A = 180० (आसन्न कोणों का योग)
समांतर चतुर्भुज के विकर्ण की लम्बाई का सूत्र | Diagonal of Parallelogram
समांतर चतुर्भुज का विकर्ण कैसे ज्ञात करते हैं:- एक समांतर चतुर्भुज का विकर्ण निम्नलिखित सूत्रों द्वारा ज्ञात किया जा सकता है।
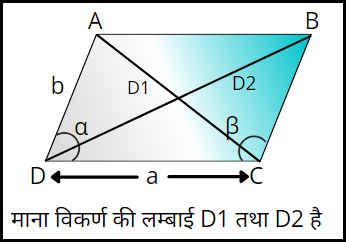
जैसा कि ऊपर दिए गए समान्तर चतुर्भुज के विकर्ण की माप D1 तथा D2 है। तब विकर्ण की माप या परिमाण निम्नलिखित सूत्रों द्वारा ज्ञात कर सकते हैं।

समांतर चतुर्भुज की विशेषता या गुण | Properties of Parallelogram in Hindi
एक समांतर चतुर्भुज की निम्नलिखित विशेषताएं होती है अतः समांतर चतुर्भुज पर आधारित प्रश्नों को हल करने से पहले निम्नलिखित गुणों को ध्यान रखना होगा।
- समांतर चतुर्भुज के आमने व सामने भुजाएं समांतर व बराबर होती हैं।
- चतुर्भुज के आमने सामने के कोणों का माप सामान होता है।
- चतुर्भुज के विकर्ण एक दुसरे को सम्द्विभाजित करते हैं।
- विकर्ण की लम्बाई आपस में बराबर नहीं होती हैं। साथ ही विकर्ण एक दुसरे लम्बवत नहीं काटते हैं।
- Samantar chaturbhuj के अन्तः कोणों का योग 360० होता है।
- एक समान्तर चतुर्भुज के आसन्न कोणों का योग सदैव 180० होता है।
- यदि एक समांतर चतुर्भुज के चारों भुजावों के मध्य बिन्दुवों को मिला दिया जाये तो बनी आकृति एक समांतर चतुर्भुज होता है।
- समांतर चतुर्भुज के दोनों विकर्ण चतुर्भुज को चार बराबर भागों में विभाजित करते हैं।
- प्रत्येक समचतुर्भुज, वर्ग तथा आयत एक समांतर चतुर्भुज होता है जिनके विकर्ण 90० पर समद्विभाजित करते हैं।
- जैसा कि नीचे दिए गए चित्र में देख सकते है यदि समांतर चतुर्भुज के अंदर कोई बिंदु (O) हो तो ऐसी स्थिति में
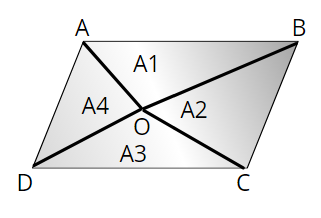
- यदि समांतर चतुर्भुज कोई भी एक कोण समकोण है तब ऐसी स्थिति में प्रत्येक कोण समकोण होगा। साथ ही बनी हुई आकृति या तो वर्ग या फिर आयत।
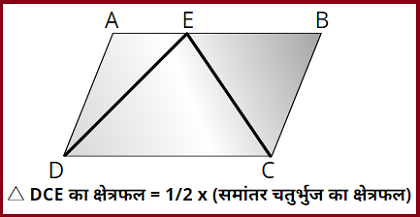
- एक समांतर चतुर्भुज के आधार भुजा पर बना हुआ त्रिभुज का क्षेत्रफल समांतर चतुर्भुज के क्षेत्रफल के आधा होता है। जैसा कि नीचे दिए गए चित्र से समझ सकते हैं।
अंत में – Samantar Chaturbhuj
मुझे आशा है कि samantar चतुर्भुज से सम्बंधित दी गयी जानकारी आपको समझ में आ गयी होगी। इसमे दी गयी बेसिक जानकारियों की मदद से इस बहुभुज पर आधारित प्रश्नों को आसानी से हल कर सकते हैं। साथ ही अन्य प्रतियोगी परिक्षावों में समांतर चतुर्भुज पर आधारित प्रश्नों को आसानी से हल कर सकते हैं।
FAQ- Formula of Parallelogram in Hindi
समांतर चतुर्भुज का क्षेत्रफल = आधार x लम्बवत ऊँचाई
समांतर चतुर्भुज का परिमित = चारों भुजावों का योगफल
समांतर चतुर्भुज के दो विकर्ण होते हैं जो कि एक दुसरे को समद्विभाजित करते हैं। साथ ही चतुर्भुज के विकर्ण की लम्बाई एक दुसरे से असमान होता है।
