Cylinder Formula – Belan ka Aaytan, kshetrafal, परिधि का फार्मूला (सूत्र):- बेलन एक त्रि-आयामी (त्रिविमीय) ज्यामिति आकृति होती है. अगर एक आयताकार चादर (Sheet या पेपर) को उसके एक शिरे (लम्बाई या चौड़ाई) के अनुदिश मोड़ा या घुमाया जाये तो जो आकृति प्राप्त होती है वो बेलन (Cylinder) होता है. बेलन आकृति ज्यामिति (Mensuration) चैप्टर का बहुत ही महत्वपूर्ण टॉपिक है. अक्सर कक्षा 9, कक्षा 10 या ने सरकारी प्रतियोगी प्रतियोगी परिक्षावों में बेलन पर आधारित प्रश्न पूछे जाते हैं. अतः ये जरुरी है की बेलन से सम्बंधित सभी मूल जानकारियां मालूम हो जैसे कि बेलन किसे कहते हैं या बेलन की परिभाषा क्या है, बेलन के आयतन का सूत्र, बेलन के वक्रपृष्ठ तथा सम्पूर्ण पृष्ठ का क्षेत्रफल का फार्मूला क्या है इत्यादि.
इस पोस्ट में बेलन से सम्बंधित सभी बेसिक जानकारियों (बेलन का आयतन, क्षेत्रफल, चित्र, परिभाषा, गुण) को साझा किया गया है. अतः दिए गए सभी बेलन फार्मूला (Cylinder Formula) को अच्छे से समझकर ही बेलन पर आधारित प्रश्नों को हल करें.
Table of Contents
बेलन – परिभाषा, वक्र पृष्ठीय क्षेत्रफल, आयतन, विशेषताएं
ठोस बेलन तथा खोखला बेलन पर आधारित सवालों को हल करने के लिए बेलन की सभी जानकारियों जानना जरुरी है. जैसे की बेलन किसे कहते है, बेलन का चित्र कैसा होता है, बेलन के कितने प्रकार होते हैं इत्यादि.
बेलन का परिभाषा | Definition of Cylinder in Hindi
सिलिंडर या बेलन किसे कहते हैं- एक बेलन तीन पृष्ठों से मिलकर निर्मित होता है. जिसमे की दो सम वृत्ताकार पृष्ठ तथा एक वक्राकर आयत होता है. अतः अगर बेलन को इस प्रकार परिभाषित किया जा सकता है कि, ” किसी आयातकार कागज या चादर के एक किनारे को स्थिर रखकर लम्बाई या चौड़ाई के अनुदिश मोड़ने पर जो संरचना (आकृति) बनती है उसे बेलन कहते हैं.”
बेलन के प्रकार | Types of Cylinder
ज्यामिति में बेलन को चार भागों में विभाजित किया जा सकता है. साथ ही बेलन के चारों प्रकार में बेलन के आयतन और क्षेत्रफल का सूत्र (Cylinder Formula) अलग अलग होता है.
- लम्ब वृत्तीय बेलन
- खोखला बेलन
- खंडित बेलन
- इलिप्टिक बेलन
सिलिंडर से सम्बंधित सभी सूत्र | Cylinder Formula
बेलन का चित्र
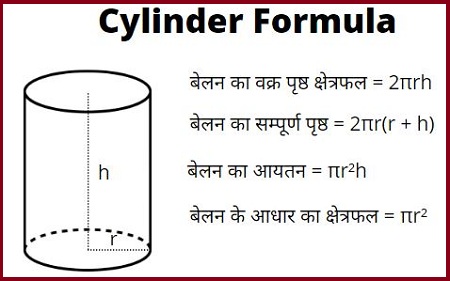
बेलन के वक्रपृष्ठ का क्षेत्रफल का फार्मूला | Curved Surface Area of Cylinder
सिलिंडर के क्षेत्रफल का Formula:- माना कि एक लम्ब वृत्तीय बेलनाकार ज्यामिति आकृति है जिसकी ऊँचाई (h) है तथा आधार वृत की त्रिज्या (r) है. तब
बेलन के वक्र पृष्ठ का क्षेत्रफल = बेलन के परिधि की लम्बाई x बेलन की ऊँचाई
बेलन का वक्र पृष्ठ क्षेत्रफल = 2 π r x h
Curved Surface Area of Cylinder = 2πrh
बेलन के सम्पूर्ण पृष्ठ के क्षेत्रफल का सूत्र | Total Surface Area Formula of Cylinder
बेलन के सम्पूर्ण पृष्ठ का क्षेत्रफल:- किसी लम्ब वृत्तीय बेलन का सम्पूर्ण पृष्ठ का क्षेत्रफल निकालने के लिए बेलन के वक्रपृष्ठ के साथ दो समतलीय वृत के क्षेत्रफल को जोड़ना होगा.
सिलिंडर या बेलन के सम्पूर्ण पृष्ठ का क्षेत्रफल = दो सम वृत्ताकार तल का क्षेत्रफल + वक्र पृष्ठ का क्षेत्रफल
बेलन के सम्पूर्ण पृष्ठ का क्षेत्रफल = 2πr2 + 2πr h
Total Surface Area of Cylinder = 2πr ( r + h )
Volume of Cylinder | बेलन के आयतन का फार्मूला
लम्ब वृत्तीय बेलन का आयतन:- एक बेलन के आयतन का तात्पर्य यह की वह बेलन कितना स्थान को घेरता है.
बेलनाकार वस्तु का आयतन = आधार वृत का क्षेत्रफल x लम्बवत ऊँचाई
बेलन के आयतन का फार्मूला = πr2 x h
Volume of right circular cylinder = πr2h
बेलन की विशेषताएं या गुणधर्म | Properties of Cylinder
एक लम्ब वृत्तीय बेलन का निम्नलिखित विशेषताएं होती हैं.
- एक बेलन दो सम वृत्ताकार तथा एक वक्राकार आयत से मिलकर बनता है.
- लम्ब वृत्तीय बेलन का आयतन πr2h होता है.
- किसी भी बेलन के लम्बवत ऊँचाई में अगर x% की वृद्धि कर दी जाये तो बेलन के आयतन में भी x% की वृद्धि हो जाएगी.
- बेलन का वक्र पृष्ठीय क्षेत्रफल 2πrh होता है जबकि सम्पूर्ण पृष्ठ का क्षेत्रफल 2πr( r + h) होता है.
- बेलन की ऊँचाई का सूत्र = (बेलन का आयतन / πr2 )
- लम्ब वृत्तीय बेलन की त्रिज्या का सूत्र = √(बेलन का आयतन / πh)
लम्ब वृत्तीय बेलन के आयतन और क्षेत्रफल पर आधारित प्रश्न
प्रश्न 1:- यदि एक बेलन की त्रिज्या आधी कर दी जाये और बेलन की ऊँचाई दो गुनी कर दी जाये तो उसका आयतन कितना होगा?
उत्तर:- त्रिज्या r = R/2 तथा h = 2H
बेलन का आयतन = πr2h = π (R/2)2 (2H)
belan ka aaytan = πr2h/2 ( बेलन का आयतन आधा हो जायेगा.)
प्रश्न 2:- दो बेलनों की त्रिज्या का अनुपात 2:3 का है तथा उनकी उंचाईयों का अनुपात 5:3 का है, तो उनके आयतनो का अनुपात ज्ञात कीजिये.
माना कि दोनों बेलनो की त्रिज्या r1 तथा r2 है और उनकी उचाईंयां h1 तथा h2 है. प्रश्न में दिया है –
r1 : r2 = 2:3 तथा h1 : h2 = 5:3
तब दोनों बेलनो के आयतन का अनुपात = (πr12h1) : (πr22h2)
या बेलनो के आयतन का अनुपात = r12h1 : r22h2 = (2/3)2 x (5/3) = 20 : 27
Cylinder Formula FAQ – बेलन के आयतन तथा क्षेत्रफल फार्मूला
यदि बेलन का आयतन या क्षेत्रफल दिया हुआ है तो बेलन त्रिज्या निकाल सकते है. माना की बेलन का आयतन दिया हुआ है तब बेलन की त्रिज्या = √{(बेलन का आयतन) /πh}
बेलन में तीन सतह होते हैं, दो सम वृत्ताकार सतह तथा एक वक्राकर आयत.
बेलन की त्रिज्या x गुनी करने पर बेलन का आयतन x2 गुना हो जायेगा.
बेलन में जो सम वृत्ताकार सतह की परिधि होती है वाही बेलन की परिधि होती है जिसका माप 2πR होता है. जहाँ R बेलन की त्रिज्या है.
एक बेलन के वक्र पृष्ठ का क्षेत्रफल 2πRh होता है,जहाँ R बेलन की त्रिज्या तथा h बेलन की लम्बवत ऊँचाई है.
